#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <sstream>
using namespace std;
struct Node {
int num;
vector<Node> child;
};
vector<Node> points;
vector<vector<int> > results;
void dfs(int u, int n, int m, int grid[][1000], bool edgest[], bool pointst[], vector<vector<int> >& ans, vector<int>& setsize)
{
if (u>m)
{
vector<int>path;
for (int i = 0; i < m; i++)
{
if (edgest[i])path.push_back(i);
}
setsize.push_back(path.size());
ans.push_back(path);
return;
}
int temp = 0;
int edge[2] = { 0 };
for (int i = 0; i < n; i++)
{
if (grid[i][u]&&!pointst[i])
{
temp++;
if (temp == 1)edge[0] = i;
else edge[1] = i;
}
}
if (temp == 2)
{
edgest[u] = true;
pointst[edge[0]] = true;
pointst[edge[1]] = true;
dfs(u + 1, n, m, grid, edgest, pointst, ans, setsize);
edgest[u] = false;
pointst[edge[0]] = false;
pointst[edge[1]] = false;
dfs(u + 1, n, m, grid, edgest, pointst,ans, setsize);
}
else
{
dfs(u + 1, n, m, grid, edgest, pointst, ans, setsize);
}
}
void pathdfs(int x, int graph[][100], int n, vector<int>&ans)
{
for (int y = 0; y < n; ++y)
{
if (graph[x][y] > 0)
{
graph[x][y]--;
graph[y][x]--;
pathdfs(y,graph,n,ans);
}
}
ans.push_back(x);
}
void ConstructPath(const vector<int>& precursor, int start, int end, vector<int>& path)
{
path.clear();
int curr = end;
while (curr != start)
{
path.push_back(curr);
curr = precursor[curr];
}
path.push_back(start);
reverse(path.begin(), path.end());
}
void Dijkstra(int start, vector<int>& distance, vector<int>& precursor, vector<vector<int> > adjacencyMatrix)
{
const int INF = INT_MAX;
int n = adjacencyMatrix.size();
distance.resize(n, INF);
distance[start] = 0;
precursor.resize(n, -1);
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > pq;
pq.push(make_pair(0, start));
while (!pq.empty()) {
int dist = pq.top().first;
int currNode = pq.top().second;
pq.pop();
if (dist > distance[currNode]) {
continue;
}
for (int i = 0; i < n; ++i)
{
if (adjacencyMatrix[currNode][i] != INF)
{
int newDistance = dist + adjacencyMatrix[currNode][i];
if (newDistance < distance[i])
{
distance[i] = newDistance;
precursor[i] = currNode;
pq.push(make_pair(newDistance, i));
}
}
}
}
}
void postman(int n,int m,int grid[][1000])
{
bool flag1 = false, flag2 = false, flag3 = false;
vector<int> path;
for (int i = 0; i < n; i++)
{
int sum = 0;
for (int j = 0; j < m; j++)
{
if (grid[i][j])
sum++;
}
path.push_back(sum);
}
int odd=0;
vector<int> oddnum;
for (int i = 0; i < n; i++)
if (path[i] % 2 == 1)
{
odd++;
oddnum.push_back(i);
}
vector<int>result;
int graph[50][100] = { 0 }, ed[50][100] = { 0 };
for (int j = 0; j < m; j++)
{
vector<int>arr;
for (int i = 0; i < n; i++)
{
if (grid[i][j])arr.push_back(i);
}
int L = arr[0], r = arr[1];
graph[L][r] = 1;
graph[r][L] = 1;
ed[L][r] = j;
ed[r][L] = j;
}
if (odd != 0)
{
int dfsgridst[100] = { 0 };
for (int i=0; i < path.size(); i++)dfsgridst[path[i]] = i;
int oddgrid[100][100] = {0};
vector<vector<vector<int> > >oddpath(odd, vector<vector<int> >(odd));
const int INF = INT_MAX;
vector<vector<int> > adjacencyMatrix(n, vector<int>(n, INF));
vector<int> ans;
for (int j = 0; j < m; j++)
{
vector<int>arr;
for (int i = 0; i < n; i++)
{
if (grid[i][j])arr.push_back(i);
}
int L = arr[0], r = arr[1];
adjacencyMatrix[L][r] = 1;
adjacencyMatrix[r][L] = 1;
}
for (int i = 0; i < n; i++)adjacencyMatrix[i][i] = 0;
for (int i = 0; i < odd; i++)
{
int start = oddnum[i];
vector<int> distance;
vector<int> precursor;
Dijkstra(start, distance, precursor, adjacencyMatrix);
for (int k = 0; k < distance.size(); k++)
{
for (int z = 0; z < odd; z++)
{
if (oddnum[z] == k)
{
oddgrid[i][z] = distance[k];
}
}
}
for (int j = 0; j < odd; j++)
{
if (i == j)
{
oddpath[i][j].push_back(0);
continue;
}
vector<int> path;
int end = oddnum[j];
ConstructPath(precursor, start, end, path);
for (int k = 0; k < path.size(); ++k) {
int x = path[k];
oddpath[i][j].push_back(x);
}
}
}
vector<vector<int> >ansdfs;
vector<int>setsize;
bool edgest[100] = { false }, pointst[100] = { false };
int dfsgrid[20][1000] = { 0 };
int eddfs[100][100] = {0};
for (int i = 0; i < odd; i++)
for (int j = 0; j < odd; j++)eddfs[i][j] = -1;
int idx = 0;
for (int p = 0; p < odd; p++)
{
for (int z = p+1; z < odd; z++)
{
if (oddgrid[p][z])
{
dfsgrid[p][idx] = 1;
dfsgrid[z][idx] = 1;
eddfs[p][z] = idx;
eddfs[z][p] = idx;
idx++;
}
}
}
dfs(0, odd, idx, dfsgrid, edgest, pointst, ansdfs, setsize);
int len = ansdfs.size();
int max = 0;
for (int i = 0; i < len; i++)
{
if (setsize[i] > max)
max = i;
}
int reslong = ansdfs[max].size();
int mindfs = INF;
int flagdfs = 0;
for (int k = 0; k < len; k++)
{
if (setsize[k] == reslong)
{
int sum = 0;
for (int i = 0; i < reslong; i++)
{
for (int edi = 0; edi < odd; edi++)
{
for (int edj = edi + 1; edj < odd; edj++)
{
if (ansdfs[k][i] == eddfs[edi][edj])
{
sum += oddpath[edi][edj].size()-1;
}
}
}
}
if (sum < mindfs)
{
mindfs = sum;
flagdfs = k;
}
}
}
vector<vector<int> >finalans;
for (int i = 0; i < reslong; i++)
{
for (int edi = 0; edi < odd; edi++)
{
for (int edj = edi + 1; edj < odd; edj++)
{
if (ansdfs[flagdfs][i] == eddfs[edi][edj])
{
finalans.push_back(oddpath[edi][edj]);
}
}
}
}
for (int i = 0; i < finalans.size(); i++)
{
for (int j = 0; j < finalans[i].size()-1; j++)
{
int Le = finalans[i][j], ri = finalans[i][j + 1];
graph[Le][ri] += 1;
graph[ri][Le] += 1;
}
}
}
vector<int> ans;
pathdfs(0, graph, n, ans);
int needlen = ans.size();
printf("\nCPP解:");
for (int i = 0; i < needlen-1; i++)
{
printf("e%d ", ed[ans[i]][ans[i + 1]]+1);
}
printf("\n");
}
void search(vector<bool> visited, int start, vector<int> rep) {
visited[start] = true;
rep.push_back(start);
bool flag = true;
for (int i=0; i<points[start].child.size(); i++) {
if (!visited[points[start].child[i].num]) {
flag = false;
search(visited, points[start].child[i].num, rep);
}
}
if (flag) {
results.push_back(rep);
}
}
struct CompareVectors {
bool operator()(const vector<int>& x, const vector<int>& y) const {
return x.size() > y.size();
}
};
int main()
{
while(1)
{
points.clear();
results.clear();
int grid[100][1000] = { 0 };
int n, m;
vector<vector<int> >ans;
vector<int>setsize;
bool edgest[100] = { false }, pointst[100] = { false };
cout << "请输入边数和点数:(输入‘0’退出)" << endl;
cin >> n;
if(n == 0) break;
cin >> m;
cout << "请输入关联矩阵:" << endl;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
cin >> grid[i][j];
}
dfs(0, n, m, grid, edgest, pointst, ans, setsize);
int len = ans.size();
int max = 0;
for (int i = 0; i < len; i++)
{
if (setsize[i] > max)
max = i;
}
int reslong = ans[max].size();
int cc = 1;
cout << endl;
for (int k = 0; k < len; k++)
{
if (setsize[k] == reslong)
{
if(cc)
{
printf("最大匹配:M = { ");
cc = 0;
}
else printf(" M = { ");
for (int i = 0; i < reslong; i++)
{
printf("e%d,", ans[k][i]+1);
}
printf("\b }\n");
}
}
unsigned int v_num = m, e_num = n;
for (int i = 0; i < v_num; i++)
{
points.push_back(Node{i});
}
for (int j = 0; j < e_num; j++)
{
vector<int> t;
for (int i = 0; i < v_num; i++) {
if (grid[i][j] == 1) t.push_back(i);
}
points[t[0]].child.push_back(points[t[1]]);
points[t[1]].child.push_back(points[t[0]]);
}
vector<bool> visited;
visited.assign(v_num, false);
for (int i = 0; i < v_num; i++) {
search(visited, i, vector<int>());
}
sort(results.begin(), results.end(), CompareVectors());
cout << "匹配数:β1 = " << results[0].size() / 2 << endl;
postman(n, m, grid);
cout << endl;
}
return 0;
}
|
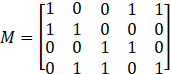 )。
)。
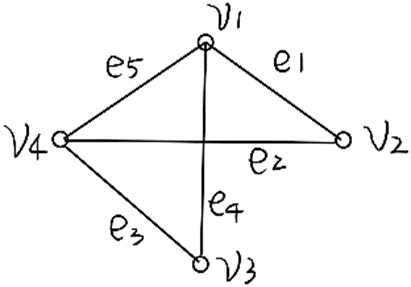


 Python 进行编程,(后面写的C++同理,就不解析了)
Python 进行编程,(后面写的C++同理,就不解析了)


